[最も好ましい] (a b c)^2 324933-A b c 2 3 a2 b2 c2
⇒ a 2 b 2 b 2 c 2 c 2 a 2 = ( ab bc ca ) 2 2 ( a 2 bc ab 2 c abc 2 ) ⇒ a 2 b 2 b 2 c 2 c 2 a 2 = ( ab bc ca ) 2 2abc ( a b c ) , Now we substitute values from equation A , 1 and 3 , we getAx 2 bx c = 0 where x is an unknown, a is referred to as the quadratic coefficient, b the linear coefficient, and c the constant The numerals a, b, and c are coefficients of the equation, and they represent known numbers For example, a cannot be 0, or the equation would be linear rather than quadratic A quadratic equation can be solved16 ejercicios resueltos productos notables nivel preuniversitarioTeoría https//wwwyoutubecom/watch?v=Qjes17MQXac

Our History Wkrn News 2
A b c 2 3 a2 b2 c2
A b c 2 3 a2 b2 c2-Answer Apply the formula a2 −b2 = (ab)(a−b) to simplify the given expression (abc)2 −(a−bc)2 = (abca−bc){abc−(a−bc)} = (2a2c)(abc−ab−c) = (2a2c)(2b) =11 Evaluate (abc) 2 = a 2 2ab2acb 2 2bcc 2 12 Evaluate (abc) 2 = a 22ab2acb 2 2bcc 2 Step 2 Pulling out like terms 21 Pull out like factors 2a 2 2b 2 4bc 2c 2 = 2 • (a 2 b 2 2bc c 2) Final result 2 • (a 2 b 2 2bc c 2)



A B C Whole Cube
Given a three variable polynomial equation Expantion of above equation can be caluculated as below Step 1expand the power of (abc)^2 (abc)^2= (abc) (abc) Step 2multiply above 2 polynomials (abc)^2=a*a a*b a*c b*a b*b b*c c*a c*b c*c Step 3add the common terms and write in a breif wayRelated example to square trinomial https//wwwyoutubecom/watch?v=lrk8I7i69LU= a 2 ab ac ba b 2 bc ca cb c 2 Adding like terms, the final formula (worth remembering) is (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ac
Start your free trial In partnership with You are being redirected to Course Hero I want to submit the same problem to Course Hero CancelFree expand & simplify calculator Expand and simplify equations stepbystepA 2 b 2 c 2 2 × 59 = 625 Given, ab bc ca = 59 a 2 b 2 c 2 118 = 625 a 2 b 2 c 2 118 – 118 = 625 – 118 subtracting 118 from both the sides Therefore, a 2 b 2 c 2 = 507 Thus, the formula of square of a trinomial will help us to expand 7th Grade Math Problems 8th Grade Math Practice
2 29 if a ib=0 wherei= p −1, then a= b=0 30 if a ib= x iy,wherei= p −1, then a= xand b= y 31 The roots of the quadratic equationax2bxc=0;a6= 0 are −b p b2 −4ac 2a The solution set of the equation is (−b p 2a −b− p 2a where = discriminant = b2 −4ac 32 Vào lúc , 1237 PM, math_galois đã nói Ngoài những hằng đẳng thức cơ bản trong sgk, còn có những hằng đẳng thức hay được sử dụng trong các bài toán như sau (1) (a b c)2 = a2 b2 c2 2ab 2bc 2ac (2) (a b − c)2 = a2 b2 c2 2ab − 2bc − 2ac (3) (a − b − c)2 = a2Click here👆to get an answer to your question ️ If a^2 b^2 c^2 = 250 and ab bc ca = 3 , then find a b c




Abc2 Closedown 14 Abc Tv Youtube




Reliability Of Abc 2 Method In Measuring Of Infarct Volume In Magnetic Resonance Diffusion Weighted Image Sananmuang T Dejsiripongsa T Keandoungchun J Apirakkan M Asian J Neurosurg
Subhikshasampath (abc) 2 =a 2 b 2 c 2 2ab2bc2ca a 2 b 2 c 2 = (abc) 2 2ab2bc2ca a 2 b 2 c 2 = (7) 2 2 (abbcca) a 2 b 2 c 2 = (7) 2 2 () a 2 b 2 c 2 = 4940 a2b2c2= 9Factor (ab)^2(cd)^2 Since both terms are perfect squares , factor using the difference of squares formula , where and Apply the distributive propertyTable For the purposes of these tables, a, b, and c represent valid values (literals, values from variables, or return value), object names, or lvalues, as appropriateR, S and T stand for any type(s), and K for a class type or enumerated type Arithmetic operators All arithmetic operators exists in C and C and can be overloaded in C
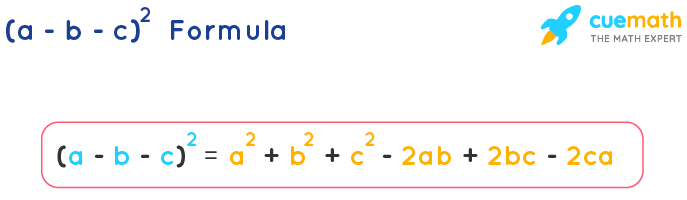



A Minus B Minus C Whole Square Formula A B C 2 Formula
/cdn.vox-cdn.com/uploads/chorus_image/image/68819263/1276896234.jpg.0.jpg)



Paulo Costa Turns Down Ufc On Abc 2 Main Event Slot Mmamania Com
(a – b – c) 2 = a 2 b 2 c 2 – 2ab 2bc – 2ca Was this answer helpful?Bảy hằng đẳng thức đáng nhớ Bách khoa toàn thư mở Wikipedia Bước tới điều hướng Bước tới tìm kiếm Trong toán học sơ cấp, bảy hằng đẳng thức đáng nhớ là những đẳng thức cơ bản nhất mà mỗi người học toán cần phải nắm vững Các đẳng thức được chứngExample 2 Solve (8x 4y 7z) 2 Solution This proceeds as Given polynomial (8x 4y 7z) 2 represents identity first ie (a b c) 2 Where a = 8x, b = 4y and c = 7z Now apply values of a, b and c on the identity ie (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ca and we get (8x 4y 7z) 2 = (8x) 2 (4y) 2 (7z) 2 2(8x)(4y) 2(4y)(7z) 2(7z)(8x) Expand the exponential forms



Free Abc Chart Pdf 25kb 1 Page S



A B C Whole Cube
Step 1 a 2 b 2 2bc c 2 Simplify —————————————————— 2 Equation at the end of step 1 (a 2b 2 2bcc 2Main article Pythagorean triple A Pythagorean triple has three positive integers a, b, and c, such that a2 b2 = c2 In other words, a Pythagorean triple represents the lengths of the sides of a right triangle where all three sides have integer lengths Such a triple is commonly written (a, b, c)Simple and best practice solution for a2b=c equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,




Abc Tv Plus Other Logopedia Fandom




Our History Wkrn News 2
Z = 2p2 − 2(a − 2b)ps 2(b2 − a2)s2 R = p2 − 2(3a − 2b)ps (4a2 − 8ab 3b2)s2 solution X = p2 2(a − 2b)ps (10a2 − 4ab − 5b2)s2 Y = 2p2 4(a b)ps (a2 − 14ab 2b2)s2 Z = − 2p2 2(a − 2b)ps (22a2 − 16ab − 2b2)s2 R = p2 2(7a − 2b)ps (4a2 8ab − 5b2)s2 solution Square Formulas (a b) 2 = a 2 b 2 2ab (a − b) 2 = a 2 b 2 − 2ab a 2 − b 2 = (a − b) (a b) (x a) (x b) = x 2 (a b) x ab (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ca (a (−b) (−c)) 2 = a 2 (−b) 2 (−c) 2 2a (−b) 2 (−b) (−c) 2a (−c) (a – b – c) 2 = a 2 b 2 c 2 − 2ab 2bc − 2ca Choose c 2 from the list of perfect squares calculated earlier Then b 2 can be calculated as b 2 = c 2 – a 2 Now check if a




1 Simplify The Following Boolean Expression Using Chegg Com



What Is The Formula For A B C Quora
B=2 C=3 D= 4 E=5 F=6 G= 7 H= 8 I=9 J=10 K=11 L=12 M=13 N=14 O=15 P=16 Q=17 R=18 S=19 T= U=21 V=22 W=23 X=24 Y=25 Z=26 Classroom Activity 2 Math 113 The Dating Game Introduction Disclaimer Although this is called the "Dating Game", it is merely intended to help the student gain understanding of the concept of Standard Deviation It is Prove that (bca2 cab2 abc2), (cab2 abc2 bca2), (abc2 bca2 cab2) is divisible by a b c and find the quotient Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesOur online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!



Home



What Is The Formula For A B C Quora
1/2 (abc)^2=a^2b^2c^22(abacbc)=0 so abacbc=1/2 (a^2b^2c^2)^2=a^4b^4c^42(a^ 2b^2a^2c^2b^2c^2)=1 so a^4b^4c^4=12(a^ 2b^2a^2c^2b^2c^2) but (abacLet a^2bc=x, b^2ca=y, c^2ab=z Then note xy=a^2bccab^2= (ab) (abc)=0yz=b^2caabc^2= (bc) (abc)=0Thus we have x=y=z We are done Let a2 − bc = x, b2 −ca = y, c2 − ab = z Then note $xy=a^2bccab^2= (ab) (abc)=0 yz=b^2caabc^2= (bc) (abc)=0 T huswehave x=y=z$ We are doneBái 1 Rút gọn các biểu thức sau 1 (abc) 2 (abc) 2 (bca) 2 (cab) 2 2 (abc) 2 (abc) 2 2 (bc) 2 3 (x1) 3 (x1) 3 6 (x1) 2 Theo dõi Vi phạm YOMEDIA Toán 8 Bài 3 Trắc nghiệm Toán 8 Bài 3 Giải bài tập Toán 8 Bài 3




Reliability Of Abc 2 Method In Measuring Of Infarct Volume In Magnetic Resonance Diffusion Weighted Image Sananmuang T Dejsiripongsa T Keandoungchun J Apirakkan M Asian J Neurosurg




Ufc On Abc 2 Predictions Who S Picking Holland To Upset Vettori
Listen to (abc)2=a2b2c2 SoundCloud is an audio platform that lets you listen to what you love and share the sounds you create 1 Followers Stream Tracks and Playlists from (abc)2=a2b2c2 on your desktop or mobile device45 (35) Upvote (33) Choose An Option That Best Describes Your Problem Answer not in Detail Incomplete Answer Answer Incorrect Others Answer not in Detail IncompleteThe a 2 b 2 c 2 formula is used to find the sum of squares of three numbers without actually calculating the squares a 2 b 2 c 2 formula is one of the major algebraic identities To derive the expansion of a 2 b 2 c 2 formula evaluate the (a b c) 2 formula Let us learn more about the a 2 b 2 c 2 formula along with solved examples What Is a^2 b^2 c^2 Formula?



Applying The Law Of Cosines Solve The Following P Gauthmath




The Branding Source New Logo Abc2
If we can show that 27 64 ( a b) 2 ( b c) 2 ( c a) 2 ≥ ( a b b c c a) 2, then the conclusion follows Denote S 1 = a b c, S 2 = a b b c c a and S 3 = a b c We need to show that 27 ( S 1 S 2 − S 3) 2 ≥ 64 S 2 3 It then goes onto prove the last inequality via casesAdditon same value\( (abc)^2 = a^2 2ab b^2 2bc 2ac c^2 \) Arrage value by Power \( (abc)^2 = a^2 b^2 c^2 2bc 2ac 2ab \) (abc)^2 Verifications Need to verify \( (abc)^2 \) formula is right or wrong put the value of a = 2, b=3 and c=4 put the value of a and b in the LHS \(=> (abc)^2 = (234)^2 \) \(=> (abc)^2 = (9)^2 \) \(=> (abc)^2 = 81 \) put the value of a and bTrả lời (1) a) ( a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ac b) ( a b c ) 2 = a 2 b 2 c 2 2ab 2bc 2ac c) (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ac bởi Thảo Tô Like (0) Báo cáo sai phạm Cách tích điểm HP Nếu bạn hỏi, bạn chỉ thu về một câu trả lời Nhưng khi bạn




A B C 2 Solve Identity Brainly In




Simplify And Factorise A B C 2 A B C 2 4b 2 4c2 Brainly In
Prove that the radius r of the circle which touches the sides of the triangle is given by r=abc/2 If a b c are sides of a triangle where c is the hypotenuse prove that the radius r of the circle which touches the sides of the triangle is given by r=abc/2 how_to_reg FollowStack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeNCERT Class 9 Maths Lab Manual – Verify the Algebraic Identity (abc)² = a²b²c²2ab2bc2ca OBJECTIVE To verify the algebraic identity (abc)² = a²b²c²2ab2bc2ca Materials Required Hardboard Coloured papers Adhesive White paper Scissors Geometry Box Prerequisite Knowledge Square and its area Rectangle and its area



1



Abc 2 Blue Lisianthus
Last updated at by Teachoo Identity V is (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ca Let us prove it Proof (a b c) 2 = ( (a b) c) 2 Using (x y) 2 = x 2 y 2 2xy = (a b) 2 c 2 2 (a b)c 66 View Full Answer N Chouhan, added an answer, on 12/3/13 N Chouhan answered this it should be 2 (a)2 (b)2 (c)= (abc)2 Was this answer helpful? a = intofloat(10) b = c * a d = e b f = d Can become b =c * 100 f = eb Phase 6 Code Generation Code generation is the last and final phase of a compiler It gets inputs from code optimization phases and produces the page code or object code as a result
:format(jpeg):mode_rgb():quality(90)/discogs-images/R-1694682-1237463159.jpeg.jpg)



Abc 2 1992 Cd Discogs



Tivvy F1uc2vpm
Basic Math Solve for b a^2b^2=c^2 a2 b2 = c2 a 2 b 2 = c 2 Subtract a2 a 2 from both sides of the equation b2 = c2 −a2 b 2 = c 2 a 2 Take the square root of both sides of the equation to eliminate the exponent on the left side b = ±√c2 − a2 b = ± c 2 a 2Short Solution Steps \frac { a ^ { 2 } } { ( a b ) ( a c ) } \frac { b ^ { 2 } } { ( b a ) ( b c ) } \frac { c ^ { 2 } } { ( c a ) ( c b ) } = ( a − b) ( a − c) a 2 ( b − a) ( b − c) b 2 ( c − a) ( c − b) c 2 = To add or subtract expressions, expand them to make their denominators the same Explanation As A B C = 3π 2, we have A B = ( 3π 2 −C) and cos(A B) = cos( 3π 2 − C) = −sinC Hence cos2A cos2B cos2C = 2cos( 2A 2B 2)cos( 2A −2B 2) cos2C = 2cos(A B)cos(A− B) cos2C



Abc 2 Blue Lisianthus




Abc Xyz Analyse To Optimize Your Inventory Abcsupplychain
If A B C = 180°, then show that cos2A cos2B cos2C = 1 – 2 cosA cosB cosCWeitzenböck's inequality $(a^2 b^2 c^2 \ge 4\sqrt{3}S)$ Two Refinements of the IonescuWeitzenbock Inequality $(a^2b^2c^2\ge 2\sqrt{3}\max\{am_a,bm_b,cm_c\})$ Another Refinement of the IonescuWeitzenbock Inequality $(\displaystyle a^2b^2c^24\sqrt{3}S\ge 2\sqrt{3}(m_a^2h_a^2))$ (a b c)² = (a² b² c²) 2(ab bc ca) 2(ab bc ca) = (a b c)² (a² b² c²) 2(ab bc ca) = 3² 5 ab bc ca = 2 Hence, 3ab 3bc




Abc Conjecture Wikipedia




In A Triangle Abc 2 Cos A Ca Cos B Ab Cos C Brainly In




Figure 3 From Comparison Of Abc 2 With The Simplified Abc 2 Formula In Calculating Intracerebral Hemorrhage Volume Semantic Scholar




Movement Assessment Battery For Children Second Edition Movement Abc 2 Pearson Assessment




Performance Characteristics Of Methods For Quantifying Spontaneous Intracerebral Haemorrhage Data From The Efficacy Of Nitric Oxide In Stroke Enos Trial Journal Of Neurology Neurosurgery Psychiatry




Abc Conjecture Wikipedia




Using Properties Of Determinant Prove That A B C B2 C2



Abc 2 Rose Lisianthus




Simplify A 2 A B C B 2 A B C C 2 A B C Brainly In
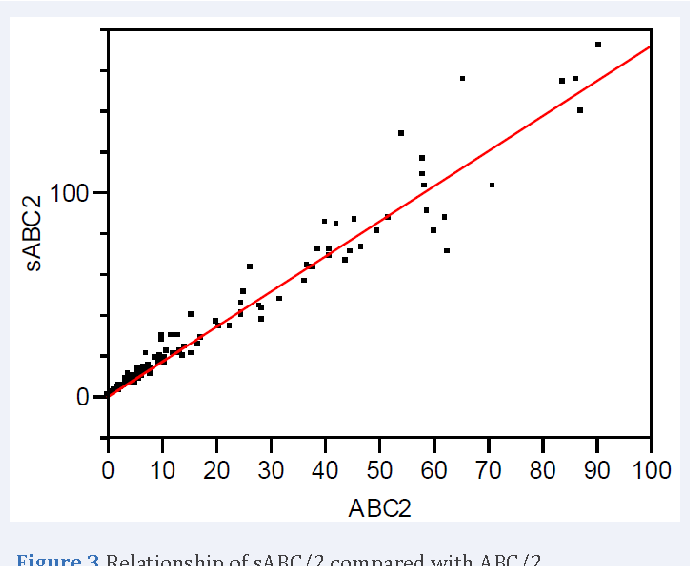



Figure 3 From Comparison Of Abc 2 With The Simplified Abc 2 Formula In Calculating Intracerebral Hemorrhage Volume Semantic Scholar




Expansion Of A B C Brainly In



Wmar 2 News Youtube




Applying The Law Of Cosines Solve The Following P Gauthmath




Figure 3 From Comparison Of Abc 2 With The Simplified Abc 2 Formula In Calculating Intracerebral Hemorrhage Volume Semantic Scholar




The Chase On Abc Cancelled Season 2 Release Date Canceled Renewed Tv Shows Tv Series Finale




Abc 2 Neurosurgery




Frequently Asked Questions Pearson Assessment




Abc Big 2 News Kmid Home Facebook



1 Abc 2 Abc 3 Abc 4 Abc



Search Q A B C 5e3 Tbm Isch




Lung Volume Reproducibility Under Abc Control And Self Sustained Breath Holding Kaza 17 Journal Of Applied Clinical Medical Physics Wiley Online Library




Ufc On Abc 2 Breakdown Can Holland S Cardio Keep Up With Vettori




Ex 4 2 7 Show Ab Ac Ba B2 Ca Cb C2 4a2b2b2
/Images/cover.jpg)



Movement Assessment Battery For Children Checklist Second Edition Movement Abc 2 Checklist Pearson Assessment



Given A Right Triangle Triangle Abc With C 90 Circ If A 2 C 6 How Do You Find B Socratic




Video Abc Launches 13 Schedule




Aberrant Behavior Checklist Second Edition Abc 2



Q Tbn And9gcsn3j5l6r4w8yyrgz Tudgwlfdwko1zokdwjjnfkgah4ccya2q8 Usqp Cau



Abc 2 Blue Lisianthus
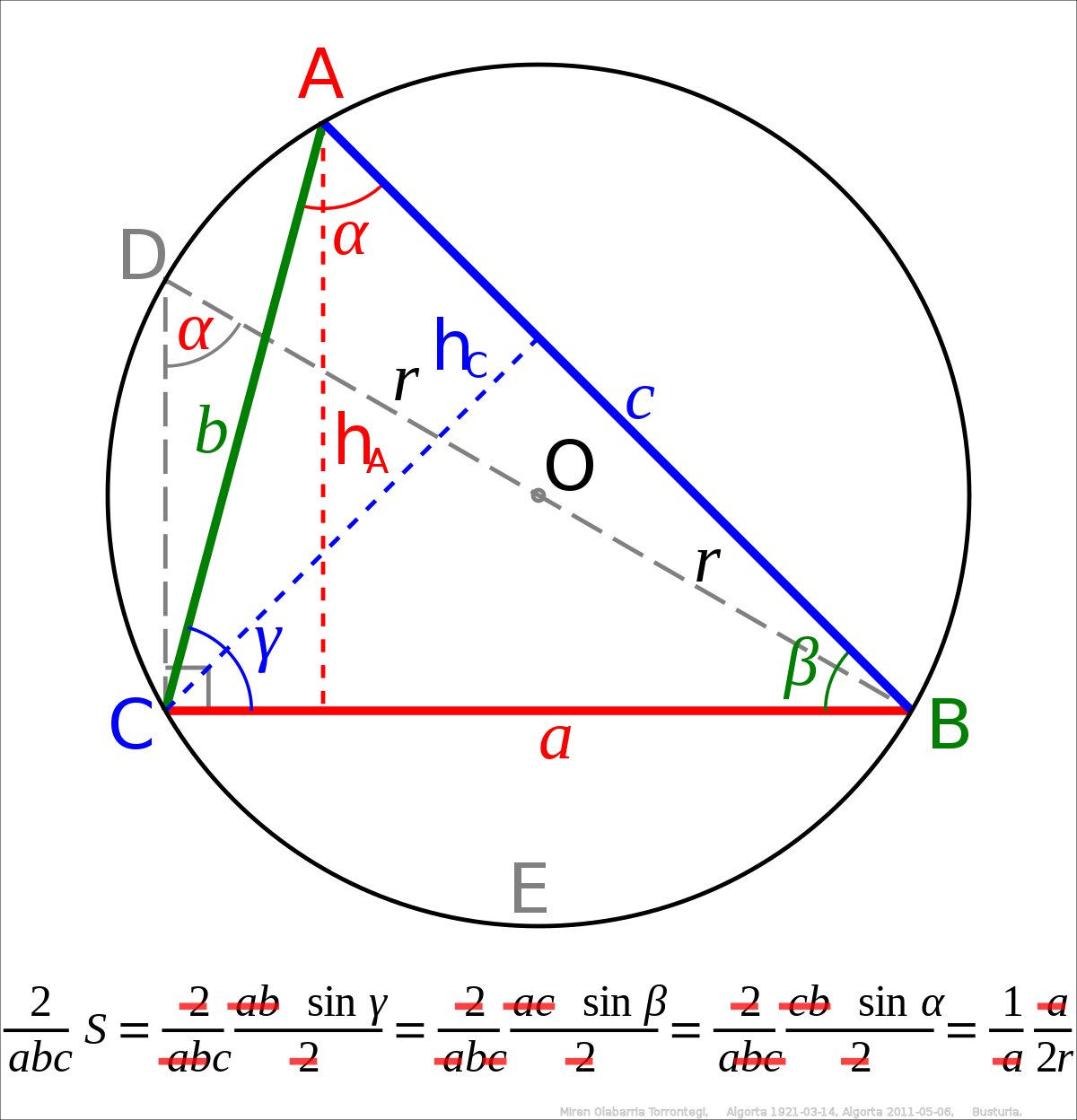



Law Of Sines Wikipedia




Frequently Asked Questions Pearson Assessment




Ufc On Abc 2 Twitter Reacts To Marvin Vettori Beating Kevin Holland




Two Dimensional 2d Arrays In C Programming With Example




Abc 2 Vector Logo Download Free Svg Icon Worldvectorlogo




Simplify A B C 2 A B C 2 Brainly In




If A B C Are Real And A 2 B 2 C 2 2 A B C 3 The Value Of 2a 3b 4c Is What Mathematics Topperlearning Com Wbihg8bb




The Vertices Of Abc Are A 2 2 B 6 2 And C 0 8 The Perimeter Of Abc Is Units And Its Area Brainly Com




Abc Tv Plus Logopedia Fandom
/s3.amazonaws.com/arc-authors/gray/95a484a6-bd51-4dd8-bcaf-ea1a0d4b11bb.png)



Abc12 Wjrt News Flint Mi



What Is The Formula For A B C Quora




Simplify A B C 2 A B C 2




Use A Truth Table To Prove That A B Ac A 1 Chegg Com
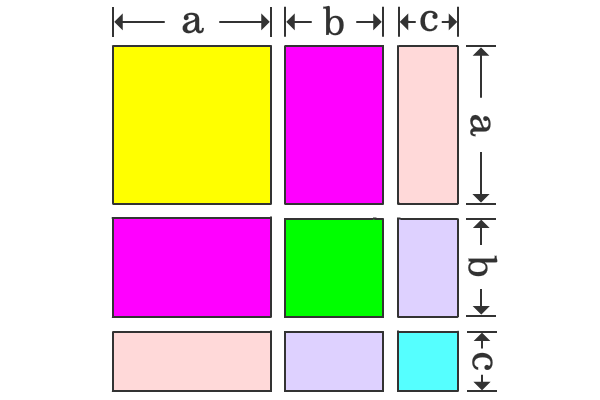



Proof Of A B C Formula In Geometric Method
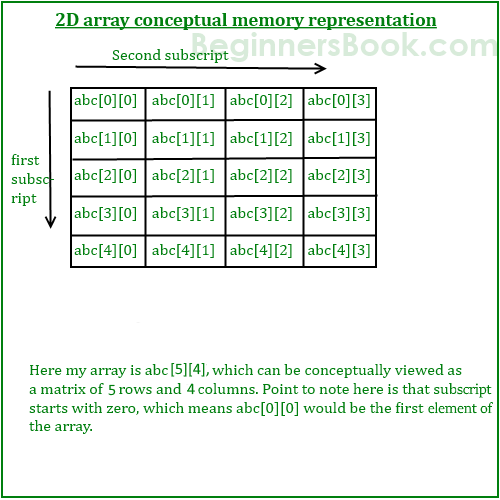



Two Dimensional 2d Arrays In C Programming With Example




Classic 2 Player Abc Classic




Baltimore News And Headlines Wmar Tv Wmar 2 News



The Abc Plus Project



How To Prove That A B B C C A A B C Quora



Geometrical Explanation Of A B C 2 Algebraic Identity Proof Derivation Math Project Youtube




Abc For Kids On 2 Logo 09 Youtube




Abc Tv Plus Other Logopedia Fandom




File Abc2 Logo Svg Wikipedia



What Is The Formula For A B C Quora



What Is The Formula Of A B C 2 Quora
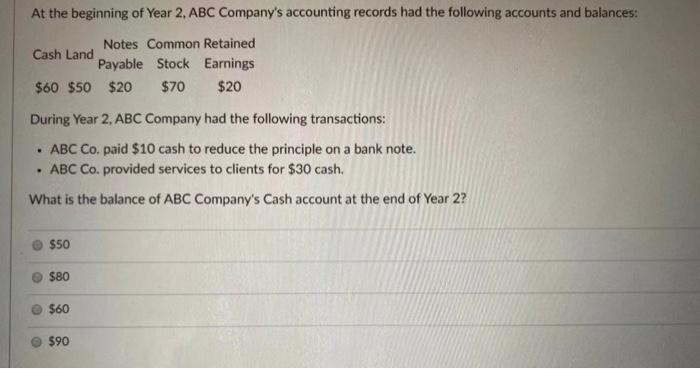



At The Beginning Of Year 2 Abc Company S Accounting Chegg Com




Formula Proof A B C 2 A 2 B 2 C 2 2ab 2bc 2ca A B C Whole Square A B C 2 Algebra Formulas Youtube




If A B C 2 Ab Ca 1 And Abc 1 And Abc 2 Find The Value Of A 3 B 3 C 3




Analyse Abc Xyz Pour Optimiser Votre Stock Abcsupplychain




Abc 2 Logo Vector Eps Free Download




Ex 14 1 1 V Find Common Factors 6 Abc 24ab 2 12 A 2b




Abc2 Closedown 30 11 17 Youtube



What Is The Formula Of A B C 2 Quora




1 Simplify The Following Expression Using Boolean Chegg Com




Abc 2 See Home Facebook
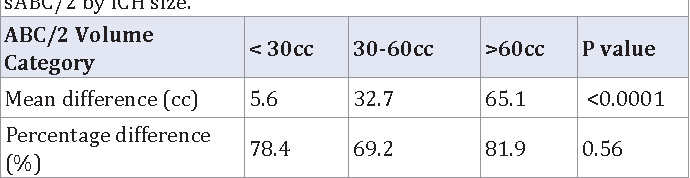



Figure 3 From Comparison Of Abc 2 With The Simplified Abc 2 Formula In Calculating Intracerebral Hemorrhage Volume Semantic Scholar



Abc 2 Rose Lisianthus




Abc Xyz Analyse To Optimize Your Inventory Abcsupplychain




Abc 2 Staines 1971 Dusashenka Flickr




Frequently Asked Questions Pearson Assessment




Movement Assessment Battery For Children Second Edition Movement Abc 2 Pearson Assessment



Simplify And Factorise A B C 2 A B C 2 4b2 4c2 Mathematics Topperlearning Com
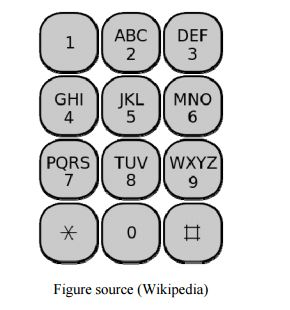



Write A Program That Takes A Phone Number 3 Digit Chegg Com



What Is The Formula For A B C 2 Quora




Abc Tv Plus Logopedia Fandom



Www Pearsonclinical Com Au Filemanager Uploads Webinar files Motor assessments for school aged children and adolescents Pdf




Expand And Simplify Trinomial Square A B C 2 A 2 B 2 C 2 2ab 2ac 2bc Youtube



Wmar Abc2 News Apps On Google Play




Wkrn News 2 Home Facebook
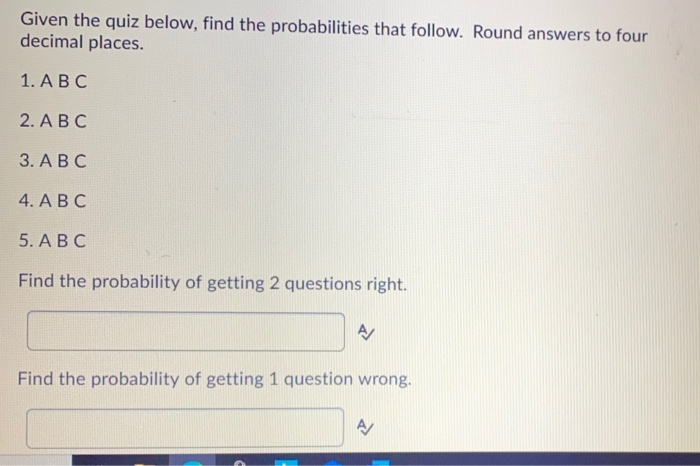



Given The Quiz Below Find The Probabilities That Chegg Com




Using Properties Of Determinant Prove That A B C B2 C2


コメント
コメントを投稿